Code Development and Numerical Simulations
Model types
Distributive numerical approaches for the simulation of flows in highly heterogeneous media have to face a variety of different scales and associated processes. To cover the broad range of requirements we develop and apply (high-performance) modeling approaches: various flavors of smoothed particle hydrodynamics models, multi-continuum models (saturated, unsaturated, hydrological coupling, surface routing), discrete fracture/fault zone models.
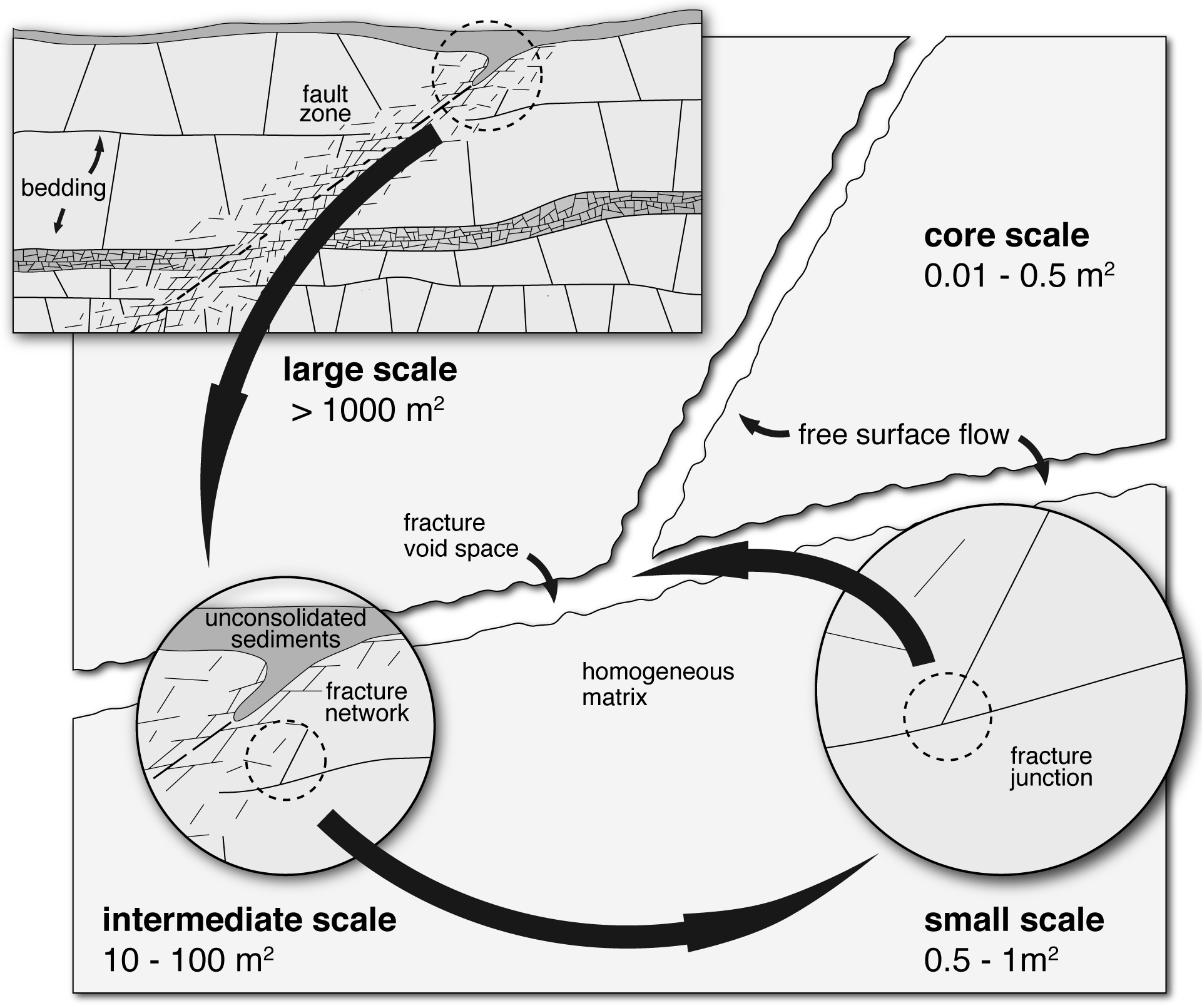
Fracture scales (Kordilla 2014)
| Model | Application Scale | Processes |
|---|---|---|
| PF-SPH (Multiscale PF-SPH*) | pore, core, small |
|
| AD-SPH | pore |
|
| Multi-Continuum | large |
|
| Discrete Fracture Models* | intermediate, large |
|
*work in progress
Smoothed Particle Hydrodynamics
In SPH, a continuous field, e.g., a fluid, is discretized with nonuniformly distributed „particles“. The term particle does not imply a specific shape (i.e., a spherical volume), but it must be understood in the sense of a mathematical integration point. Particles interact via the so-called kernel, which is used to obtain a smoothed value of the respective field variables using the weighted contribution of surrounding particles The velocity is given by the well-known Navier-Stokes (linear momentum conservation) equation
\( \frac{d\mathbf{v}}{dt} = -\frac{\nabla P}{\rho} + \frac{\mu}{\rho}\nabla^2 \mathbf{v} + \mathbf{g} \)
and the continuity equation
\( \frac{d\rho}{dt} = -\rho(\nabla \cdot \mathbf{v}) \)
For SPH models this can be discretized using the SPH formalism to yield
\( \frac{d\mathbf{v}_i}{dt} = \sum_{j=1}^N m_j \left( \frac{P_i}{\rho_i^2} + \frac{P_j}{\rho_j^2} \right) \mathbf{\hat{e}}_{ij} \frac{\partial W(\mathbf{r}_{ij},h)}{\partial r_{ij}} \)
\( + \sum_{j=1}^N m_j \frac{\mu_i+\mu_j}{\rho_i \rho_j} \frac{\mathbf{v}_{ij}}{r_{ij}} \frac{\partial W(\mathbf{r}_{ij},h)}{\partial r_{ij}} + \mathbf{g} \)
which allows the simulation of flows governed by classical newton mechanics.
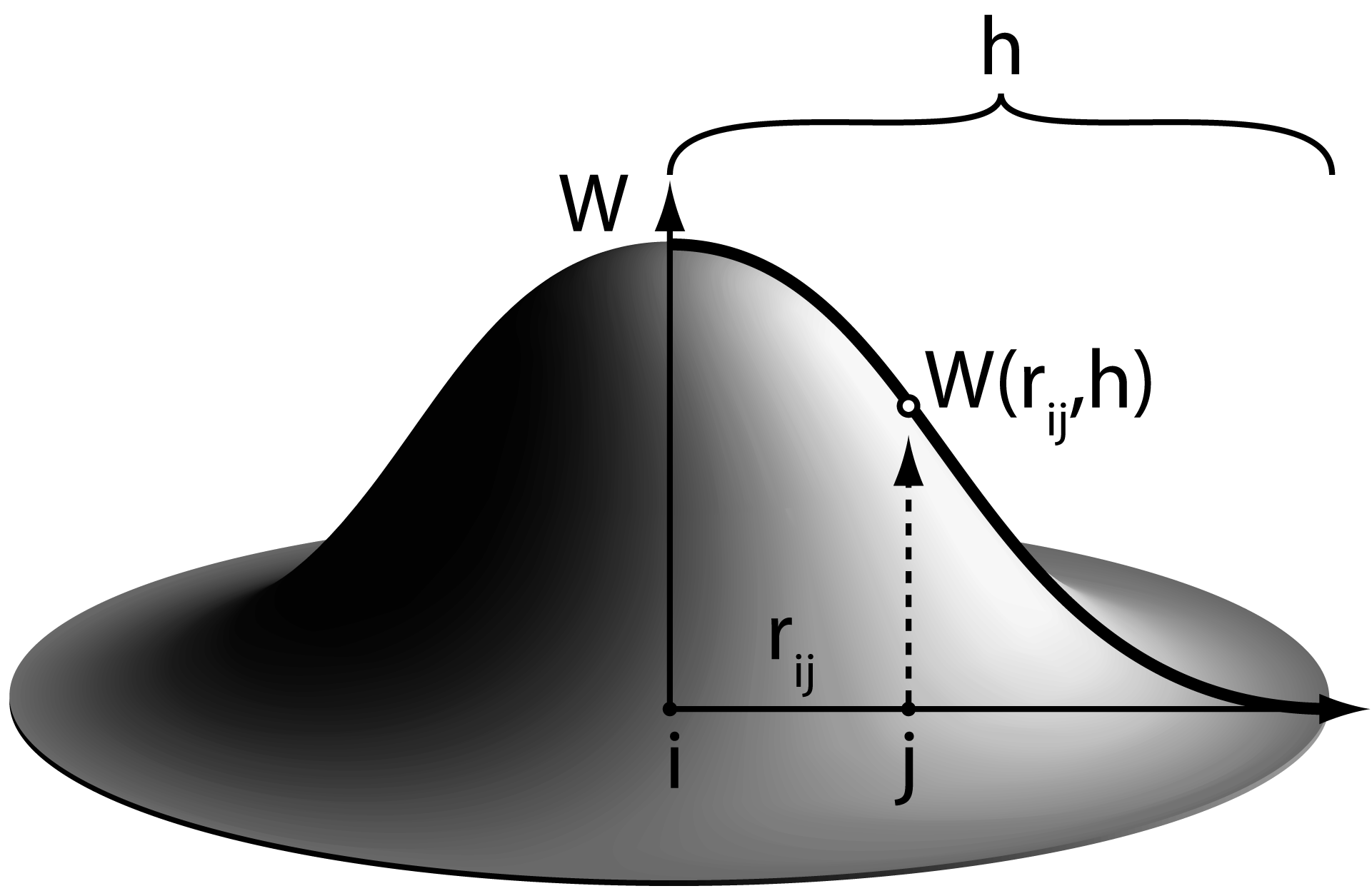
SPH interaction kernel (Kordilla 2014)
PF-SPH
PF-SPH, due to the efficient use of pairwise interaction forces with a short-range repulsive and long-range attractive component
\( \frac{d\mathbf{v}_i}{dt} = … + \sum_{j=1}^N\frac{1}{m_j} \mathbf{f}_{ij} \)
allows simulation of highly dynamics pore scale flows including the effects of surface tension. Specifically in wide aperture fracture systems this approach becomes highly efficient as there is no need to discretized an air-phase. Our current code is fully integrated into the highly efficient MPI-parallelized LAMMPS framework and allows the simulation of systems with several hundred million to billion particles. Due to the adaptive MPI-loading mechanisms also complex geometries with sparsely populated domains (as in the case of free-surface flows) can be simulated with excellent scaling properties. We have studied various processes and phenomena contributing to unsaturated flow in fractures and have extensively validated our code:
- dependence of gravity-driven flow modes on fracture intersection partitioning dynamics
- fracture filling dynamics along preferential flow paths
- effects of (fractal) surface roughness on unsaturated flow dynamics
- effects of roughness orientation on flow dynamics
- hydrophilicity/hydrophobicity effects of rough surfaces
- static and dynamic contact angle hysteresis of wetting and non-wettings fluids
- dimensionless scaling properties of droplet dynamics
- dependence of trailing droplet film formation on system geometry and fluid properties
- effects of (pre-)wetted fracture surfaces on flow velocites
In our recent DFG project we develop a multiscale SPH model to couple flow dynamics in a porous matrix system with rapid gravity-driven flow dynamics in adjacent fractures. Due to the strong scale-contrasts with respect to the average void space between matrix and fracture a bruteforce discretization of the whole system is not feasible on todays computing systems. Instead we rely on classical Richards-type matrix flow coupled to the Lagrangian SPH description of free-surface flows.
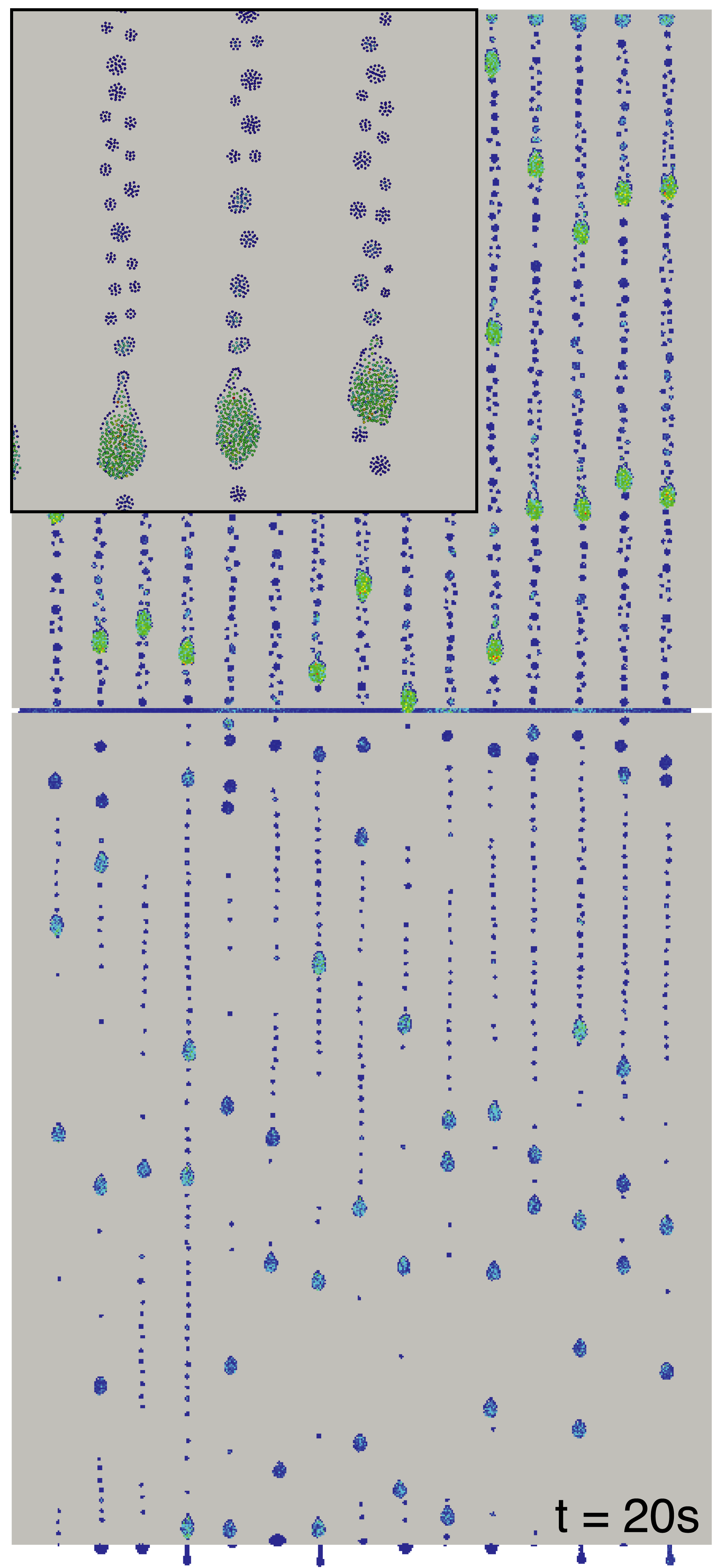
Flow along a vertical surface intersected by a horizontal fracture with about 3 million particles (Kordilla et al. 2017)
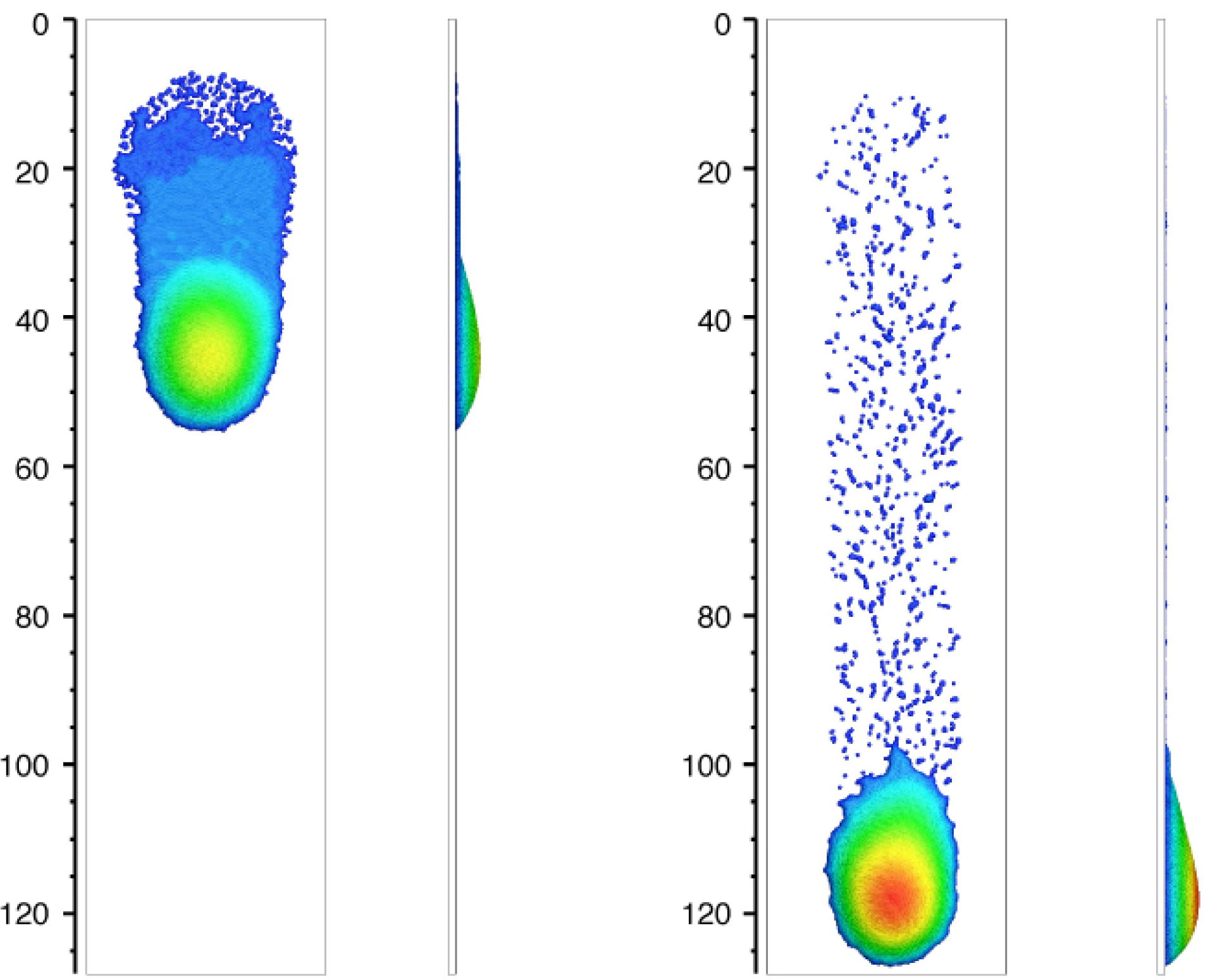
Dynamic formation of wetting films (Kordilla et al. 2013)

Flow through synthetic rough fracture arrays (Bresinsky 2017, M.Sc. thesis)
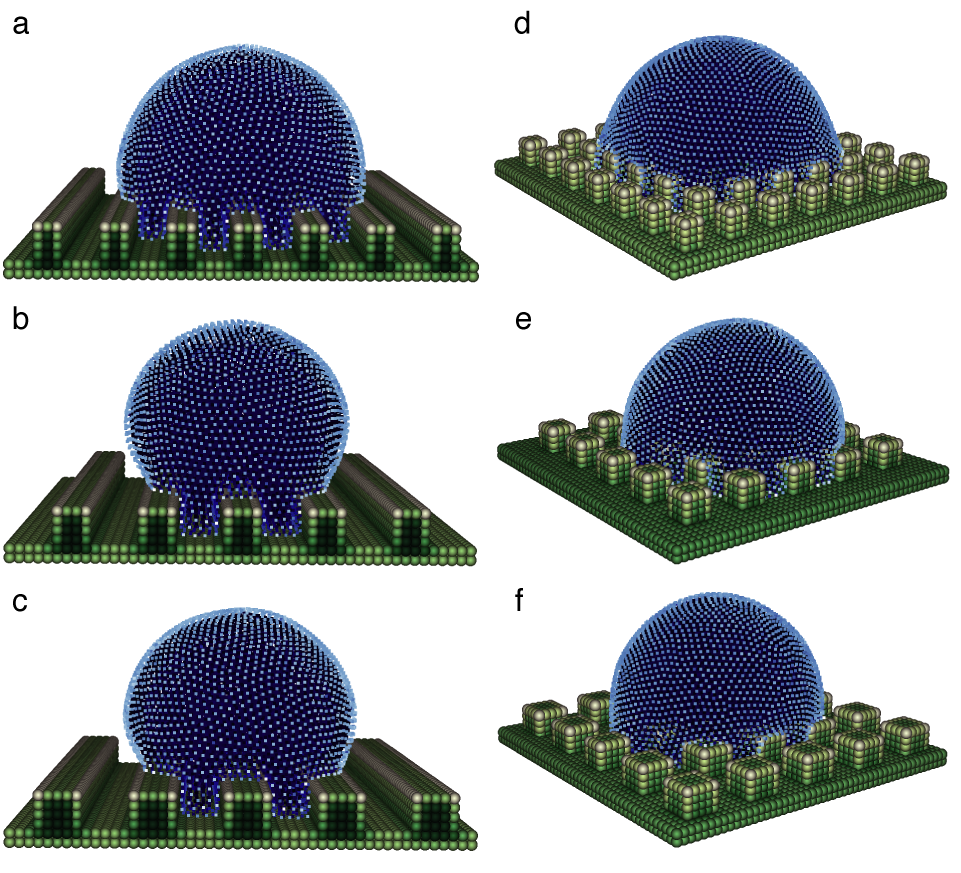
Effects of microscopic roughness patterns on macroscopic apparent contact angles (Shigorina et al. 2017)

Various degrees of fractal surface roughness (Kordilla 2017, unpublished)
AD-SPH
Advection-Diffusion-SPH (Kordilla et al. 2014) is a discretization of the fully coupled Landau-Lifshitz-Navier-Stokes (LLNS) and stochastic advection-diffusion equations. It allows the simulation of diffusion and advective transport processes on arbitrary macroscopic (Fickian diffusion) to microscopic (atomistic) scales where the hydrodynamic behavior begins to be dominated by thermal fluctuations governed by the fluctuation-dissipation theorem. The additional random forces are added to the momentum-conservation equation following the classical SPH formalism in symmetric form:
\( \mathbf{F}_i^{\xi} = \sum_{j=1}^{N}\left(\frac{\boldsymbol{s}_j}{n_{j}^2}+\frac{\boldsymbol{s}_i}{n_{i}^2}\right)\cdot \frac{\mathbf{r}_{ij}}{r_{ij}}\frac{ d W(r_{ij},h)}{d r_{ij}} \)
where the magnitude of the random stress is scale- and timestep dependent and the lm-component of the stress tensor is given by
\( s^{lm}_i = \sqrt{ \frac {4 h^3 \mu \widetilde{k}_B T \delta^{lm} n_i^2}{\Delta t } } \xi_i^{lm} \)
with a unit-variance random number \( \xi \). Our model is able to properly recover all fundamental spatial statistics induced by fluctuations and associated divergence of the interface power spectrum and its scale-invariant nature of the perturbed surfaces. Despite the microscopic nature it is remarkable that gravitational effects are strong enough to dampen the evolution of the interfaces.
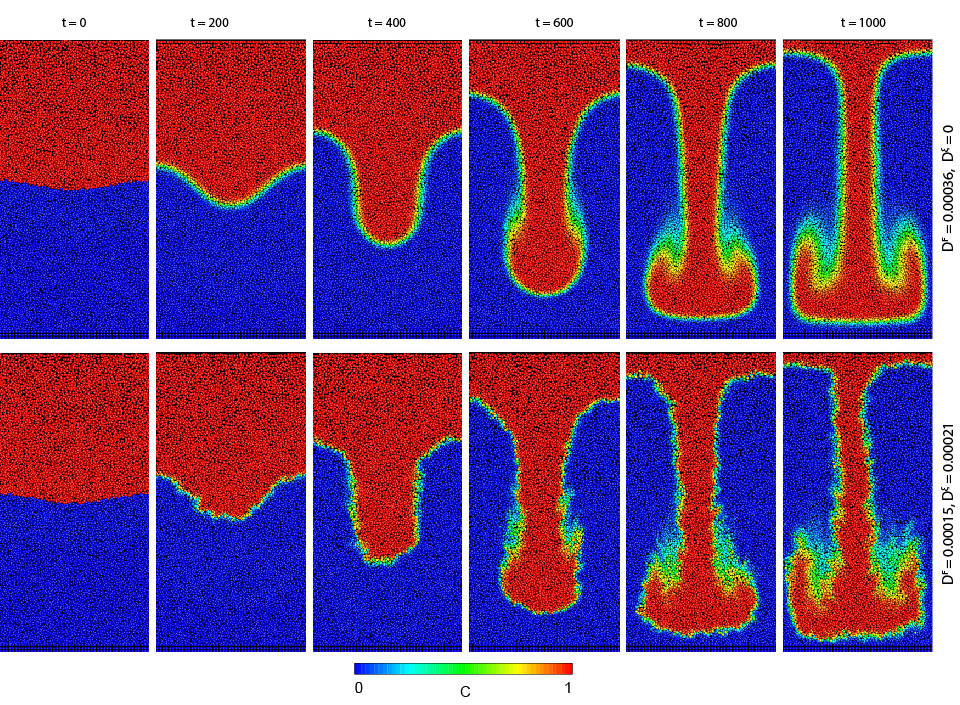
Rayleigh-Taylor instability (top SPH, bottom AD-SPH, Kordilla et al. 2014)
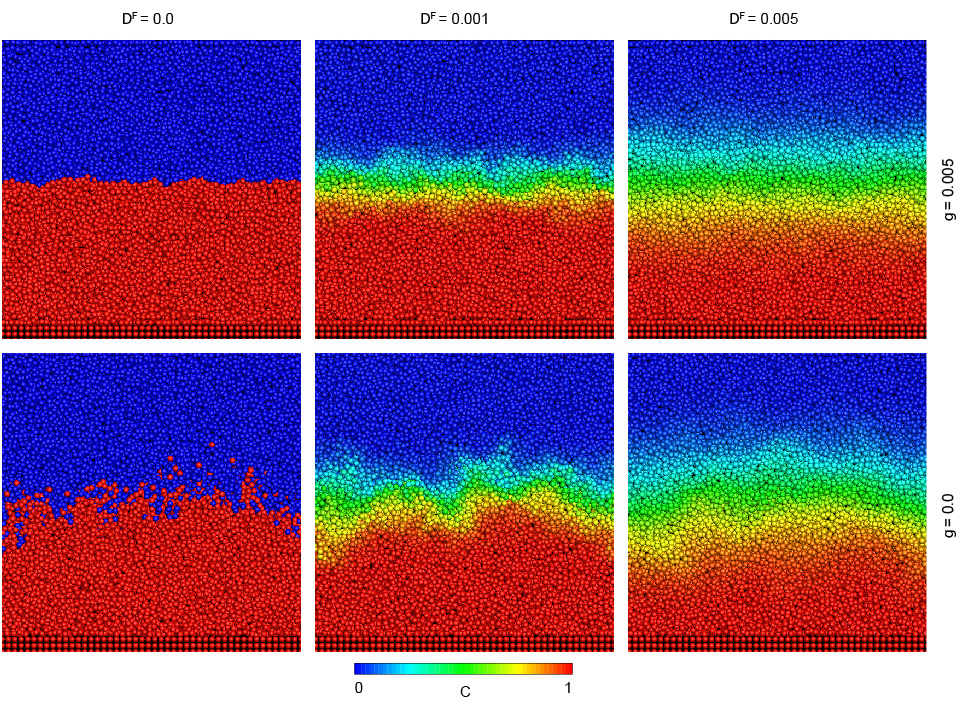
Development of a front driven by a concentration gradient (top SPH, bottom AD-SPH, Kordilla et al. 2014)
Multi-Continuum Modeling
We are currently involved in the modeling of karst and fractured aquifers, amongst others in Israel, France and India. Due to limitations in computational capacities and/or data provision it is often not feasible to explicitly resolve individual fractures, karst conduits or other highly conductive pathways in distributive modeling approaches. Nevertheless, while the exact location and geometry of such features is often difficult to detect, they may clearly dominate the shape of spring signals, control the aquifer response of hydraulic tests and can be recognized in tracer studies and associated arrival times.
Dual-continuum (multi-continuum) models rely on a decomposition of the model into a set of hydraulically interacting domains \(d=1,…,n\), each with a volumetric fraction of the total porosity \(w_d\), specific hydraulic properties (flux \(q_d\), storage terms \(S\)) and coupled by a suitable exchange coefficient \(\Gamma_{ex}\).
\( -\nabla w_d(q_d) + \Gamma^{ex} \pm R_d = w_d \frac{\delta \theta_d^s S_d^w}{\delta t} \)
This allows modeling of complex aquifer dynamics, including the karst-specific rapid system reaction followed by a slower porous matrix dominated recession period. Transport dynamics, such as environmental tracer routing or contamination simulations, which often exhibit a clear coupling between porous matrix and the highly conductive fracture system, can easily be modeled as well.
Furthermore we are interested in the coupling of hydrological surface flow and vadose recharge dynamics, specifically in (semi-)arid regions where the limited precipitation volumes are often highly concentrated (spatially and temporally) and trigger a variety of challenging processes during the routing from surface to water table.
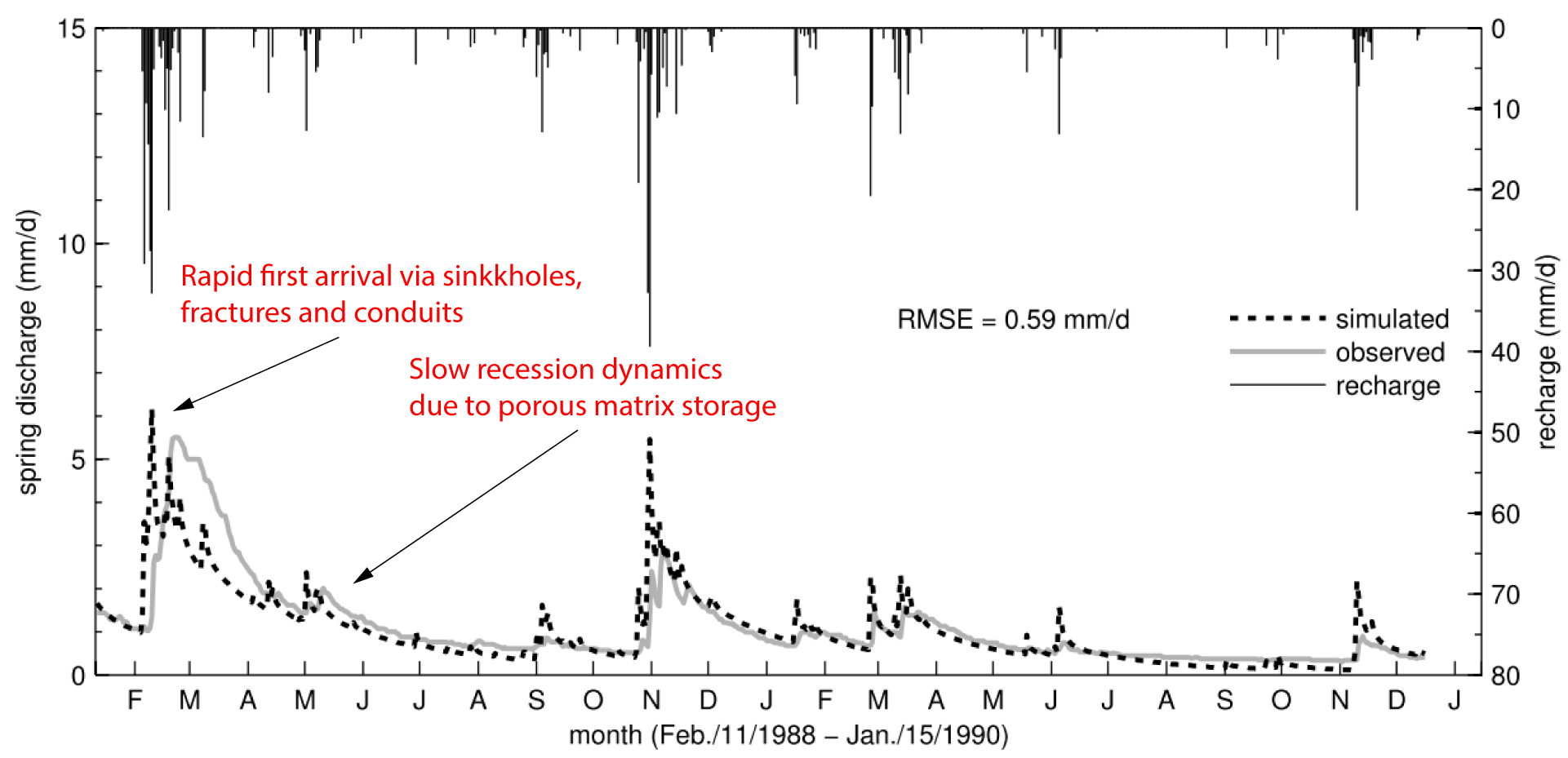
Duality of hydraulic pathways and charactersistic spring discharge features (Kordilla et al. 2012)
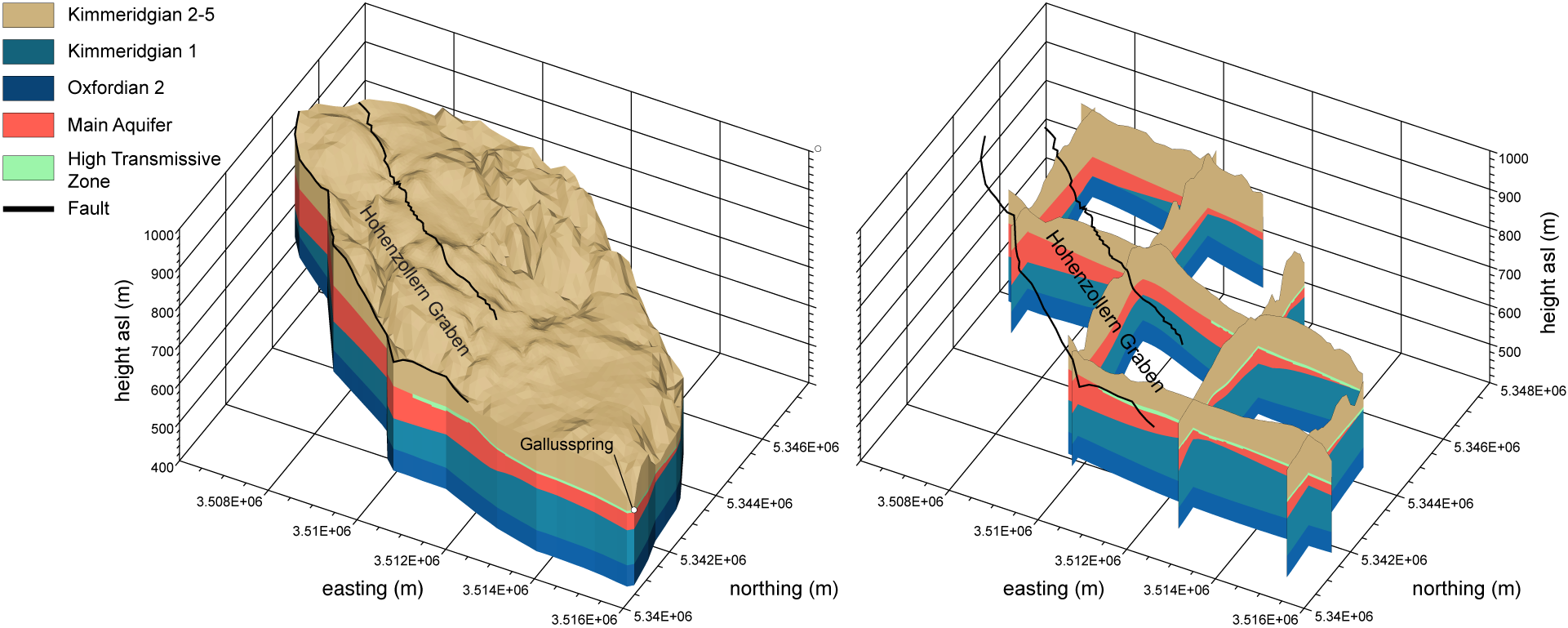
Gallusspring, Germany, 3D Hydrogeological Model (Kordilla 2012)
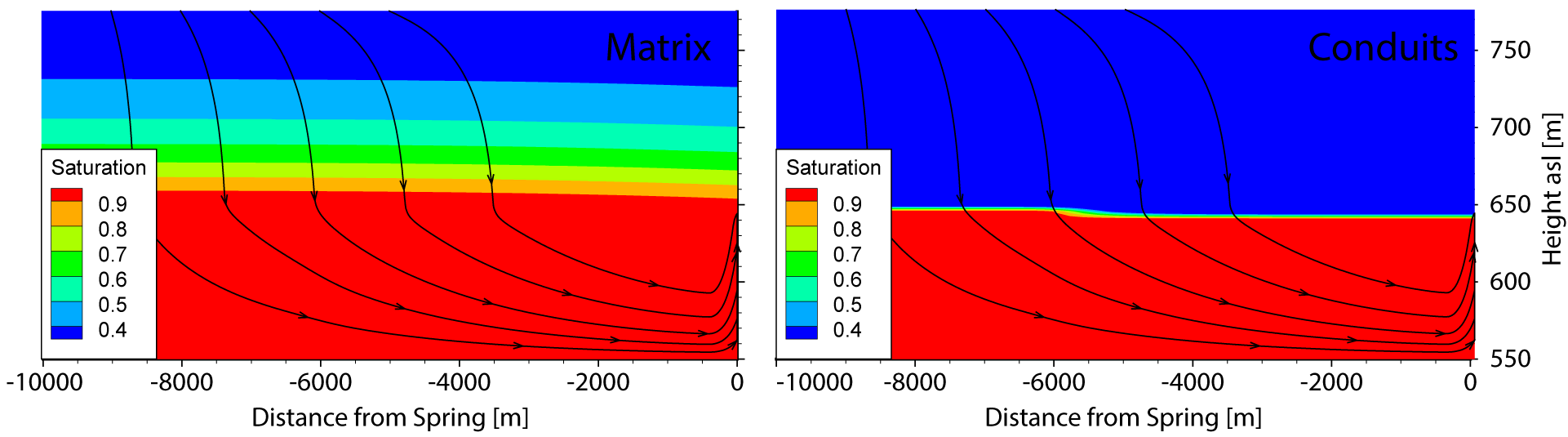
Galluspring 2D Model, Dual-continuum Saturation (Kordilla 2012)
Discrete Fracture Modeling
Discrete fracture network or fault zone models commonly employ a classical parallel plate description based on the Navier-Stokes equation to model aperture-dependent fluid flow within highly conductive elements embedded in a porous matrix:
\( Q = -\frac{\rho g}{12\mu} \frac{\Delta h}{\Delta x} (2h)^2 A \)
Compared to discrete approaches such as SPH they are numerically more efficient but do not account for internal fracture flow dynamics, flow modes or other similar features.
We apply discrete models to get a better understanding of infiltration dynamics on outcrop and catchment scales. The connection between fracture (network) geometry/topology and the formation of preferential flow paths (flow instabilities) in fractured-porous media is still an open question and requires further research on numerical implementation, analytical modeling as well as (analogue) laboratory and field experiments.
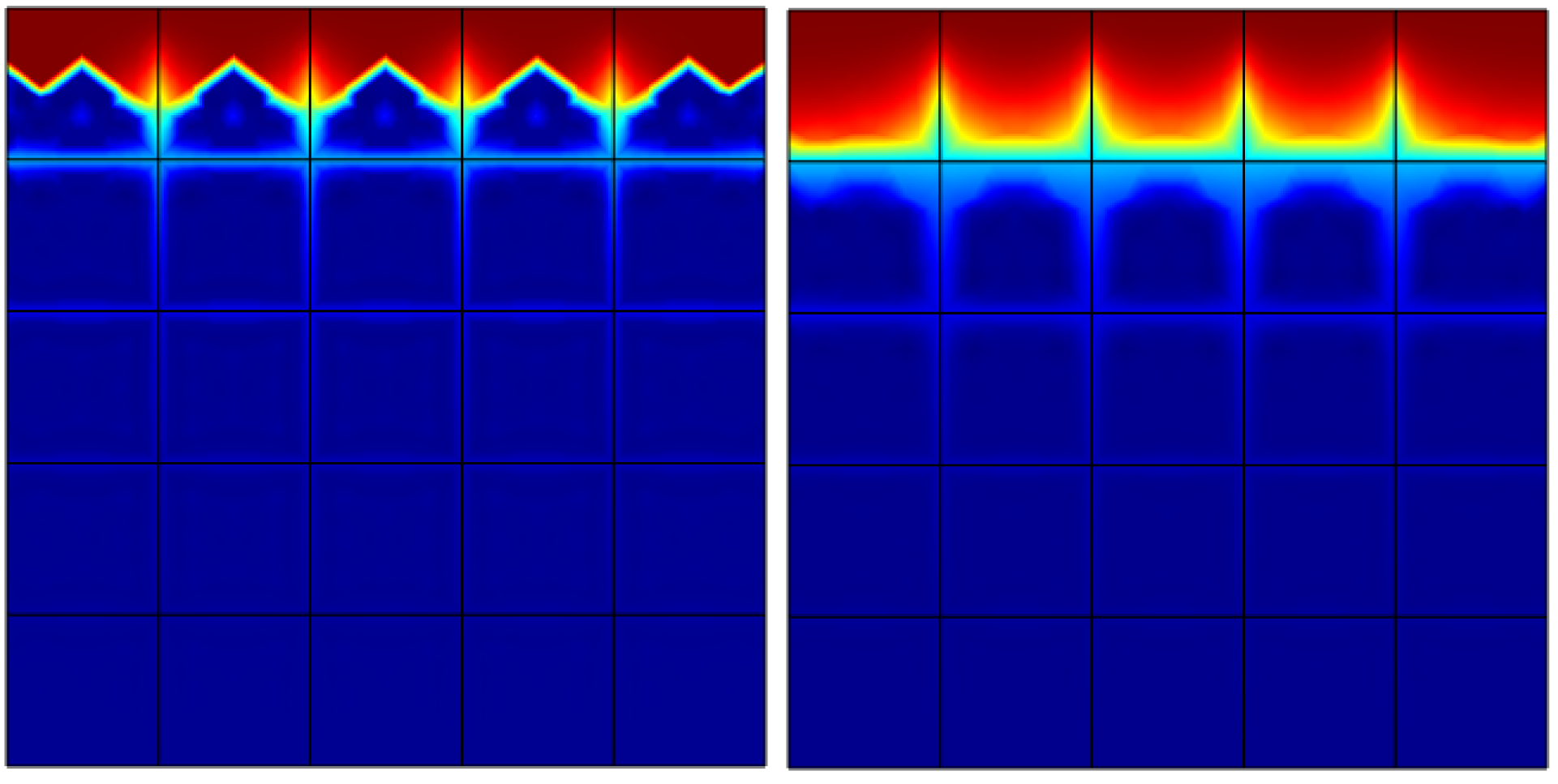
Infiltration dynamics through unsaturated discrete fracture networks (Tariq 2017, M.Sc.)
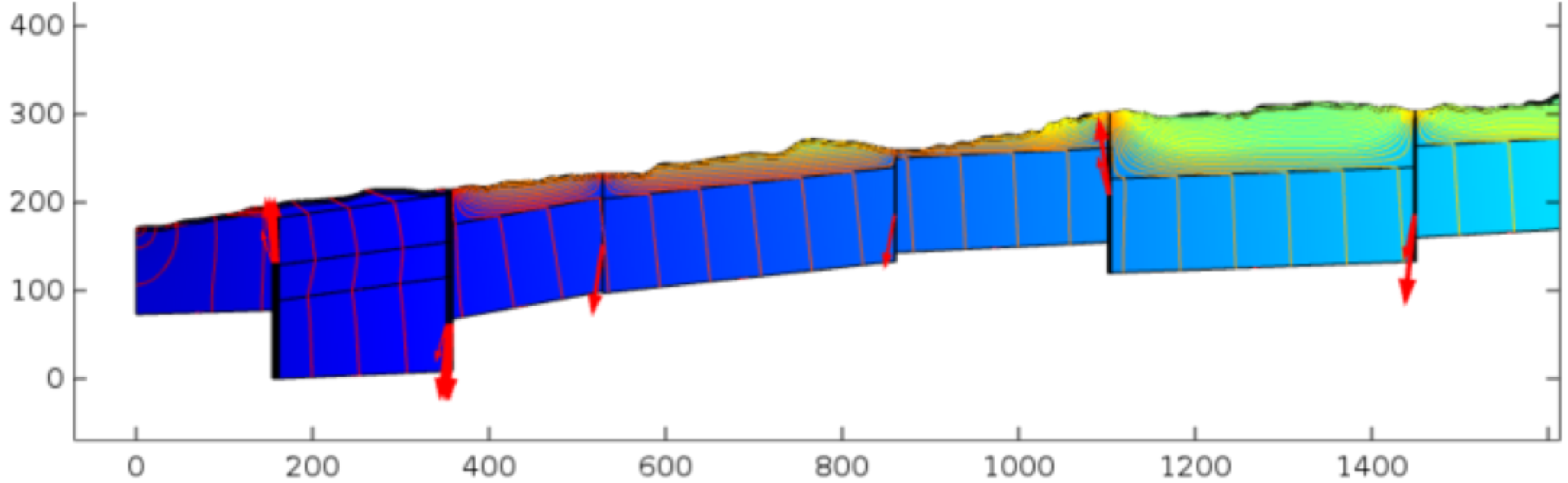
Flow model for a catchment with heavy fault and graben structures (Terrell 2017, M.Sc.)